
يمثل العثور على تحدٍّ رياضي جيد هدفاً دائماً لعالم الحاسوب مارجين هول. يعمل هول أستاذاً مساعداً في جامعة كارنيجي ميلون، ويتمتع بصيت ذائع في حل المعضلات الرياضية باستخدام الأدوات الحاسوبية. وعلى سبيل المثال، فقد تمكن في 2016 من حل “معضلة الثلاثيات البوليانية الفيثاغورية” بإثبات هائل شكل مادة دسمة للعناوين الصحفية: إثبات رياضي هو الأضخم على الإطلاق بحجم 200 تيرابايت. والآن، يعمل على تطبيق طريقة مؤتمتة لحل فرضية كولاتز التي توحي بالبساطة بشكل مخادع.
وقد طُرحت هذه الفرضية لأول مرة (وفقاً لبعض المصادر) في الثلاثينيات من قبل عالم الرياضيات الألماني لوثار كولاتز، وهي معضلة في نظرية الأعداد تتضمن وصفة، أو خوارزمية، لتوليد تسلسل رقمي. ويكفي أن تبدأ مع أي عدد صحيح وموجب. فإذا كان زوجياً، اقسمه على اثنين. وإذا كان فردياً، اضربه بثلاثة واجمعه مع الواحد. وقم بإعادة العملية مراراً وتكراراً. وتنص الفرضية على أن هذا التتابع سينتهي على الدوام بالرقم 1 (ومن ثم سيدخل في حلقة مفرغة من الأرقام 4، 2، 1).
وعلى سبيل المثال، فإن الرقم 5 يولد فقط ستة عناصر:
5، 16، 8، 4، 2، 1
أما الرقم 27 فيولد تتابعاً بطول 111 رقماً، متذبذباً صعوداً وهبوطاً، ويصل إلى قيمة عليا تساوي 9,232، قبل أن ينتهي به المطاف إلى الرقم 1.
ويولد الرقم 40 تتابعاً قصيراً آخر:
40، 20، 10، 5، 16، 8، 4، 2، 1
وحتى اليوم، تم التحقق من صحة الفرضية باستخدام الحواسيب انطلاقاً من جميع القيم الأولية الممكنة وصولاً إلى ما يقارب 300 مليار مليار، وجميع هذه الأرقام ولدت تتابعات انتهت بالرقم 1.
“ما نحاول فعله هو تحديد الطرف الأكثر براعة في حل هذه المعضلات: البشر أم الحواسيب؟”.
– مارجين هول
ويعلق هول قائلاً: “وهو محق على الأرجح”. فبالنسبة لهول، فإن جاذبية فرضية كولاتز لا تتعلق بكونها إنجازاً جديداً بقدر ما تتعلق بإحراز تقدم في تقنيات المعالجة المنطقية. وبعد العمل على هذه المسألة لمدة خمس سنوات، قام هول وشريكاه سكوت أرونسون وإيمري يولكو مؤخراً بنشر بحث في خادم arXiv للأبحاث العلمية في مرحلة ما قبل النشر. وكتب الباحثون: “على الرغم من أننا لم ننجح في إثبات فرضية كولاتز، فنحن نعتقد أن الأفكار المُقدمة هنا تمثل مقاربة جديدة مثيرة للاهتمام”.
يقول أرونسون، وهو عالم حاسوب في جامعة تكساس في أوستن: “إنه فشل مشرّف”. وهو فشل بطبيعة الحال لأنهم لم يتمكنوا من إثبات الفرضية فعلياً. غير أنه مشرف لأنهم أحرزوا تقدماً من ناحية أخرى: حيث ينظر إليه هول على أنه انطلاقة نحو تحديد الأفضل في إثبات هذه المسائل: البشر أم الحواسيب.
نقل الرياضيات نحو الحوسبة
بالنسبة للكثير من المسائل الرياضية، فإن الحواسيب تقف مكتوفة الأيدي، لأنها لا تستطيع الوصول إلى كامل الأعمال الرياضية المتراكمة عبر التاريخ. ولكن، وفي بعض الأحيان، تنقلب الآية، وتصبح الحواسيب بالغة البراعة حيث يعجز البشر. فإذا وصفنا شكل الحل للحاسوب -أي حددنا له الهدف ومساحة بحث واضحة- فقد يتمكن من إيجاد الحل بطريقة القوة العمياء، أي تجريب جميع الحلول الممكنة حتى العثور على الحل الصحيح. ولكن، ما زال الجدل قائماً حول صحة إضافة النتائج المحوسبة إلى بنية العمل الرياضي الشاملة؛ حيث تقول وجهة النظر التقليدية إنه لا يمكن توسيع حدود الرياضيات إلا بالاعتماد على الابتكار والتفكير البشري عبر المفاهيم والأفكار، في حين أن التطورات في الحوسبة تُستبعد بوصفها أعمالاً هندسية لا أكثر.
“يكمن جمال الطريقة المؤتمتة في أنك تستطيع تشغيل الحاسوب والاكتفاء بالانتظار وحسب”.
– جيفري لاجارياس
يتمتع هول بخبرة كبيرة مع أداة حاسوبية تسمى “نظام حل سات” أو “نظام الحل وفق المعايير”، وهو برنامج حاسوبي يحدد وجود حل معادلة أو معضلة وفق مجموعة من القيود. ولكن، وفي حالة تحدٍّ رياضي، يحتاج استخدام نظام حل سات أولاً إلى ترجمة أو تمثيل المسألة بشكل يفهمه الحاسوب. وكما يقول يولكو، وهو طالب دكتوراه مع هول: “التمثيل مسألة هامة للغاية”.
نجاح مستبعد، ولكنه يستحق المحاولة
عندما تحدث هول لأول مرة عن حل فرضية كولاتز باستخدام نظام حل سات، كانت أول فكرة خطرت على بال أرونسون: “من المستحيل بأي حال أن تنجح هذه المحاولة”. غير أنه اقتنع بسهولة أن المسألة تستحق المحاولة، بما أن هول تمكن من اكتشاف أساليب مبتكرة لتحويل هذه المعضلة القديمة إلى شكل يمكن أن يجعلها قابلة للحل؛ فقد لاحظ أن علماء الحاسوب كانوا يستخدمون أنظمة حل سات بنجاح لاكتشاف إثباتات انتهاء لتمثيل مجرد للحسابات باسم “نظام إعادة الكتابة”. لقد كان احتمال النجاح مستبعداً، ولكنه اقترح على أرونسون أن تحويل فرضية كولاتز إلى نظام إعادة كتابة يمكن أن يساعد في الحصول على إثبات انتهاء لهذه الفرضية، ومن الجدير بالذكر أن أرونسون كان قد ساعد في السابق على تحويل فرضية ريمان إلى نظام حاسوبي، وقام ببرمجته في آلة تيورينج صغيرة. في تلك الأمسية، قام أرونسون بتصميم النظام. ويقول: “لقد كان الأمر أشبه بفرض منزلي أو تمرين ممتع”.
“لقد كنت أتعارك، وبشكل حرفي، مع المُنهي – ترمينيتور (في إشارة طريفة إلى شخصية الأفلام الشهيرة)، أو على الأقل مع نظام إثبات نظرية انتهاء”.
– سكوت أرونسون
وقد جرب هول استخدام أحدث أدوات إثبات انتهاء أنظمة إعادة الكتابة، ولكنه لم ينجح، وهو ما كان مخيباً للآمال، على الرغم من أنه لم يكن مفاجئاً. يقول هول: “هذه الأدوات مصممة على وجه الخصوص لمسائل يمكن حلها في دقيقة، في حين أن أي مقاربة لحل فرضية كولاتز ستحتاج على الأرجح إلى أيام -بل وربما سنوات كاملة- من الحسابات”. وهو ما مثل بالنسبة له حافزاً على تطوير وتحسين هذه المقاربة، وتطبيق أدواته الخاصة لتحويل معضلة إعادة الكتابة إلى معضلة حل وفق المعايير.
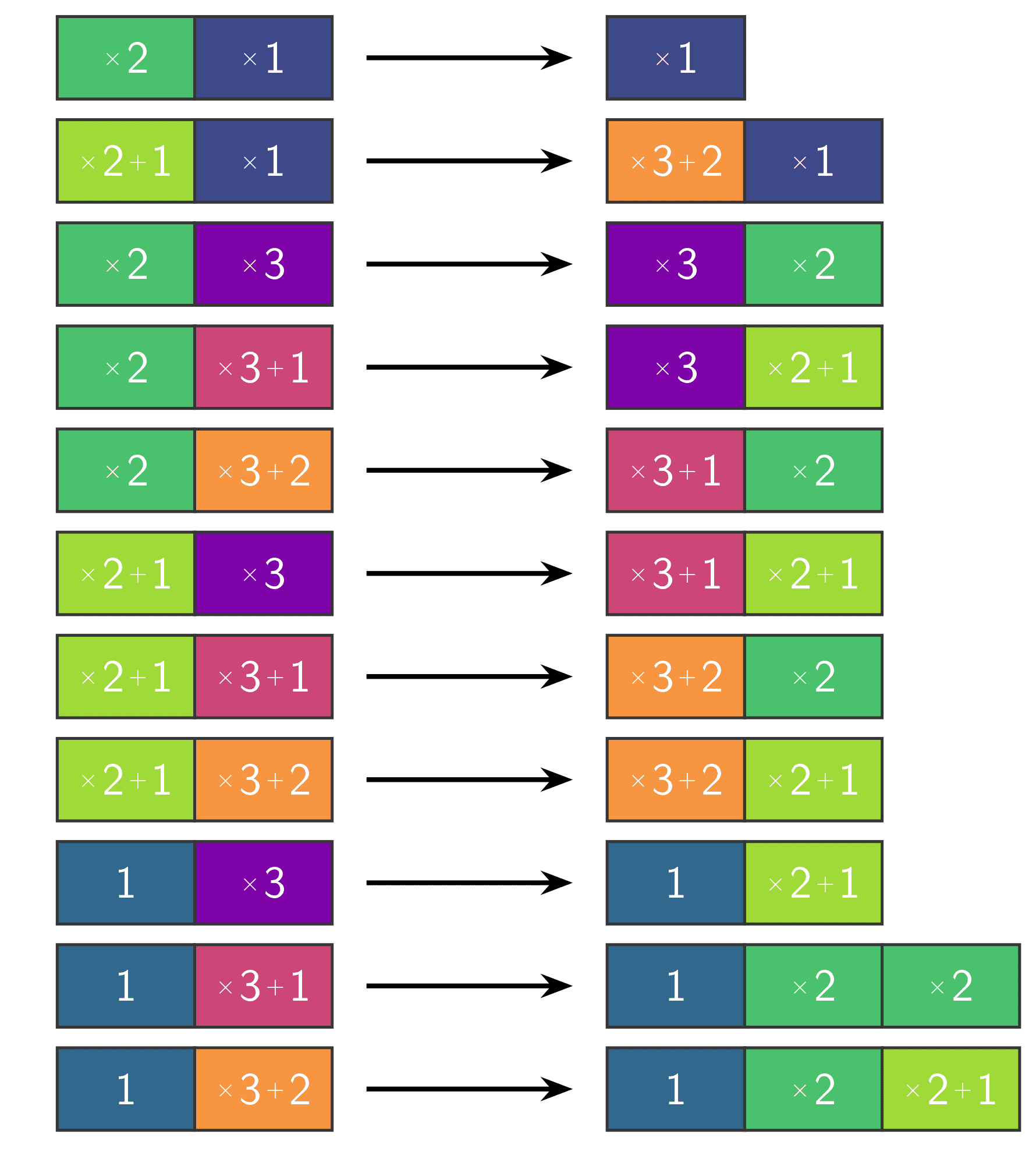
مصدر الصورة: مارجين هول
استنتج أرونسون أنه قد يكون من الأسهل بكثير حل النظام بالاستغناء عن إحدى القواعد الإحدى عشر، وذلك للحصول على نظام شبيه بكولاتز لإجراء اختبار أولي كمرحلة تحضيرية لتحقيق الهدف الأكبر. وهكذا، أطلق تحدياً بين الحاسوب والبشر: حيث حدد الطرف الرابح بأنه الطرف الذي ينجح في حل جميع الأنظمة الفرعية بعشر قواعد فقط. وجرب أرونسون حلها باليد. في حين جرب هول استخدام نظام الحل سات؛ فقد قام بترميز النظام كمسألة تحقيق معايير، غير أنه أضاف طبقة ذكية أخرى من التمثيل، حيث حول النظام إلى لغة مفهومة بالنسبة للحاسوب عن طريق مجموعة من المتحولات التي تأخذ قيمتين فقط، الصفر والواحد، ومن ثم بدأ بتشغيل نظام حل سات على نوى المعالجة للبحث عن إثبات الانتهاء.
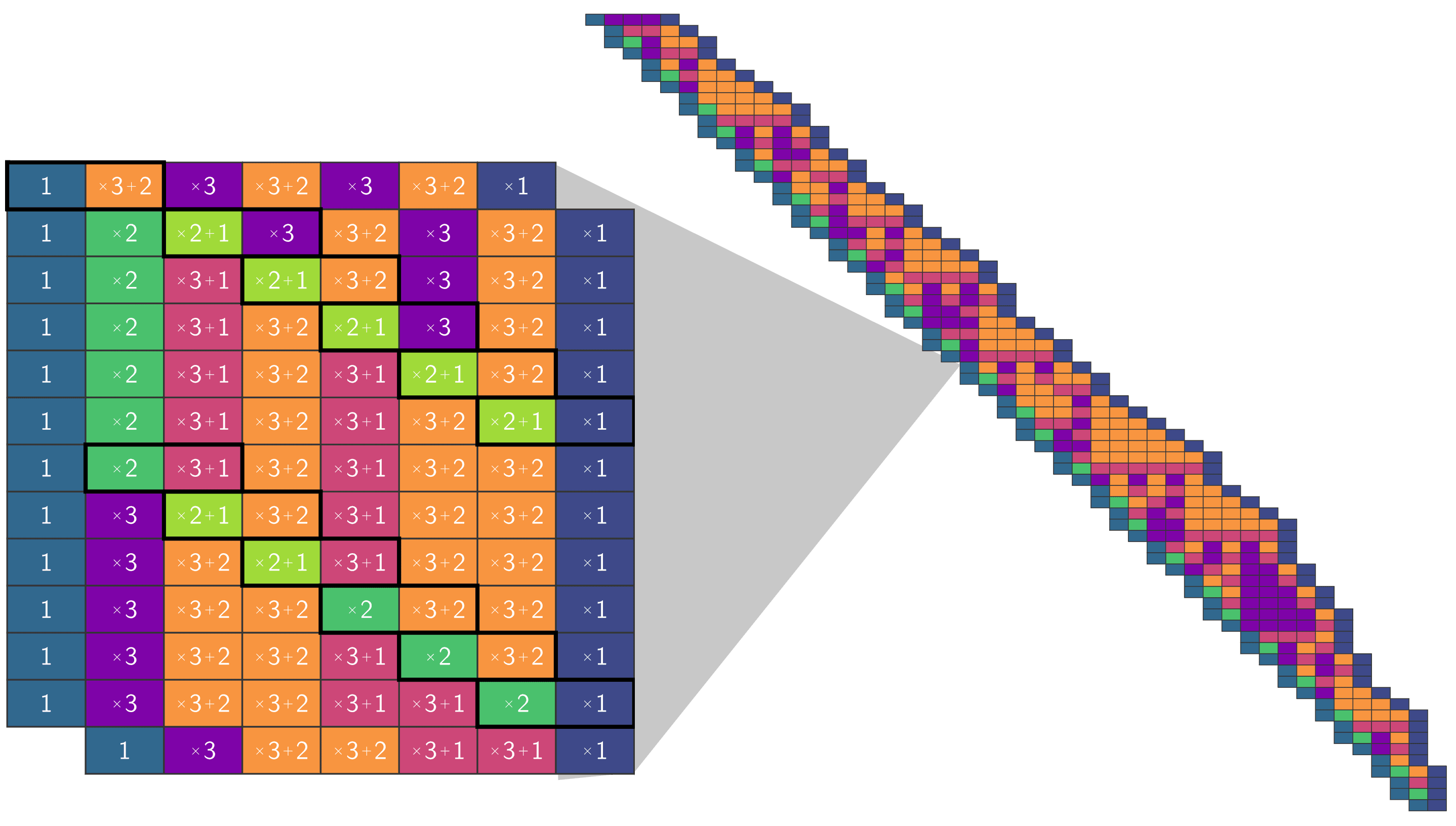
مصدر الصورة: مارجين هول
نجح كلاهما في إثبات انتهاء النظام مع مجموعات مختلفة مؤلفة من 10 قواعد. وفي بعض الأحيان، كانت المهمة سهلة للغاية، سواء بالنسبة للبشر أو البرنامج. وقد تطلبت طريقة هول المؤتمتة 24 ساعة على الأكثر. أما طريقة أرونسون فقد احتاجت إلى جهد عقلي كبير؛ حيث احتاجت إلى عدة ساعات، أو حتى يوم كامل، وقد عجز عن إثبات إحدى مجموعات القواعد العشر، على الرغم من أنه يعتقد بقوة أنه كان قادراً على ذلك بمزيد من الجهد. ويقول: “لقد كنت أتعارك، وبشكل حرفي، مع المُنهي – ترمينيتور (في إشارة طريفة إلى شخصية الأفلام الشهيرة)، أو على الأقل مع نظام إثبات نظرية انتهاء”.
منذ ذلك الحين، قام يولكو بتحسين نظام حل سات، ومعايرة الأداة حتى تصبح أكثر توافقاً مع طبيعة مسألة كولاتز. وقد أحدثت هذه الحيل فرقاً كبيراً، حيث أدت إلى تسريع إثباتات الانتهاء للأنظمة الفرعية بعشر قواعد، وتخفيض زمن العمل إلى عدة ثوانٍ وحسب.
يقول أرونسون: “أما السؤال الذي ما زال دون إجابة: ماذا عن المجموعة الكاملة من 11 قاعدة؟ إذا حاولت تشغيل النظام على المجموعة الكاملة، فسوف يعمل دون توقف، وهو ما ليس بالأمر المفاجئ، لأنها معضلة كولاتز”.
وبرأي هول، فإن معظم الأبحاث في مجال التفكير المنطقي المؤتمت تتجاهل المسائل التي تحتاج إلى الكثير من الحوسبة. ولكن، وبناء على إنجازاته السابقة، فهو يعتقد أن هذه المسائل قابلة للحل. لقد قام آخرون بتحويل كولاتز إلى نظام لإعادة الكتابة، ولكن يمكن بناء زخم واضح نحو الحل عن طريق إستراتيجية استخدام نظام حل سات مع معايرة دقيقة على مستوى عالٍ مع قوة حوسبة كبيرة.
حتى الآن، قام هول باستخدام حوالي 5,000 نواة في عمله على فرضية كولاتز، وهي وحدات المعالجة التي تعتمد عليها الحواسيب، ويوجد منها في الحواسيب الاستهلاكية عادة أربع أو ثمانية نوى. وبوصفه عضواً في برنامج أمازون سكولارز، فهو يحمل دعوة مفتوحة من خدمات أمازون ويب لاستخدام موارد “تكاد تكون غير محدودة”، يمكن أن تصل إلى مليون نواة. ولكنه متردد إزاء استخدام عدد أكبر بكثير من الأنوية.
ويقول: “أرغب في رؤية ما يشير إلى أنها ستكون محاولة واقعية ويمكن أن تؤدي إلى نتيجة”. وإلا، فسوف يكون هذا العمل مجرد إضاعة للموارد والثقة، كما يشعر. “لا أريد تأكيداً كاملاً، ولكنني أرغب في رؤية دليل على وجود احتمال معقول للنجاح”.
دفع التحول إلى الأمام
يقول الرياضي جيفري لاجارياس من جامعة ميشيغان: “يكمن جمال الطريقة المؤتمتة في أنك تستطيع تشغيل الحاسوب والاكتفاء بالانتظار وحسب”. لقد جرب لاجارياس العديد من الطرق والأساليب على فرضية كولاتز لمدة حوالي 15 سنة وأصبح بمنزلة مرجع في هذه المسألة، فراكم العديد من الكتابات الأكاديمية، كما قام بتحرير كتاب حول الموضوع باسم: التحدي الأكبر (The Ultimate Challenge)، وبالنسبة للاجارياس، فإن الطريقة المؤتمتة تذكره ببحث يعود إلى العام 2013 للرياضي جون هورتون كونواي من برينستون، الذي كان يعتقد أن معضلة كولاتز قد تكون جزءاً من صنف فريد من نوعه من المسائل الصحيحة و”غير القابلة للحسم”، ولكن من المؤكد أنها غير قابلة للحسم بالإثبات. وكما يقول كونواي: “قد تكون الفكرة القائلة بأن هذه المسائل غير قابلة للإثبات هي نفسها أيضاً غير قابلة للإثبات، وهكذا دواليك”.
يقول لاجارياس: “إذا كان كونواي محقاً، فلن يكون هناك إثبات، سواء أكان مؤتمتاً أو غير ذلك، ولن نعرف الجواب أبداً”.
بالنسبة للكثيرين، يُعد الرياضي تيرينس تاو، من جامعة كاليفورنيا لوس أنجلوس، أقرب البشر إلى الحل؛ ففي 2019 أثبت تاو أن فرضية كولاتز “شبه” صحيحة بالنسبة لجميع الأرقام “تقريباً”، مستخدماً -كما هو واضح- تقريبين مختلفين لمعاني المصطلحات الواردة في نص الفرضية.
يعتقد تاو أن الإثبات البشري للفرضية يحمل أهمية أكبر من الإثبات الحاسوبي؛ حيث سيوضح السبب الحقيقي لصحتها. ويقول: “ولكن الاعتماد على نظام حل مؤتمت للتعامل مع مسألة كبيرة قد يؤدي إلى دفع التحول إلى الأمام بشكل ثوري من حيث طريقة استخدام الرياضيين للحواسيب في مساعدتهم على عملهم. وبوجود مسألة بهذا الاستعصاء، نحن مستعدون للقبول بأية نتائج يمكن الحصول عليها”.
غير أن ما يسعى هول وزملاؤه فعلياً إلى تحقيقه هو بناء سيناريو -باستخدام هذه الطريقة مع هذه المسألة- ينجح فيه الحاسوب حيث يفشل البشر، أو العكس. يقول هول: “حالياً، لا نعرف ما إذا كانت تلك التقنيات أكثر جدوى مما يستخدمه البشر في حساباتهم اليدوية، أم أن البشر يستطيعون القيام بأشياء يعجز عنها الحاسوب. ما نحاول فعله هو تحديد الطرف الأكثر براعة في حل هذه المعضلات: البشر أم الحواسيب؟”.
ولهذا، لنرَ من سينجح في حل معضلة كولاتز أولاً.
